Tento článok pozostáva z 3 častí:
- Analýza pôvodného článku a metódy
- Štatistická simulácia metódy a jej vyhodnotenie
- O čo vlastne ide a závery
Teraz sa pozrieme na simuláciu tejto metódy. Kompletný zdrojový kód nájdete ako IPython Notebook.
Nasledujúca časť je však to podstatné. Implementácia logiky uvedenj metódy.
{% highlight python linenos %} def play(tosses, account_balance): # account_history podrzi vsetky hodnoty uctu pocas celej hry account_history = [account_balance] # pociatocna uroven stavky je 1 euro bet = 1 # stavkujeme na cervenu alebo na ciernu, zaciname na ciernej betting_on_red = False # vyhrali sme toto kolo? won = False
# iterujeme cez vsetky nahodne hody
for num in tosses:
# ak prave stavkujeme na cervenu a padla cervena, vyhravame
if betting_on_red and num in red:
won = True
# ak stavkujeme na ciernu a padla cierna, tiez vyhravame
elif not betting_on_red and num in black:
won = True
# inak sme prehrali
else:
won = False
# ak sme toto kolo vyhrali
if won:
# pripiseme si vyhru
account_balance += bet
# zmenime farbu
betting_on_red = not betting_on_red
# resetujeme stavku na 1 euro
bet = 1
# ak sme prehrali
else:
# odpocitame si prehru
account_balance -= bet
# zvysime stavku na dvojnasobok
bet *= 2
# zapiseme si vysledok do historie
account_history.append(account_balance)
# ak sme klesli s uctom na alebo pod nulu, koncime
if account_balance <= 0:
return account_balance, account_history
# vratime vysledky
return account_balance, account_history
{% endhighlight %}
Ak z tohoto kódu vynecháme riadky 56 a 57, môžeme dostať nasledujúci graf
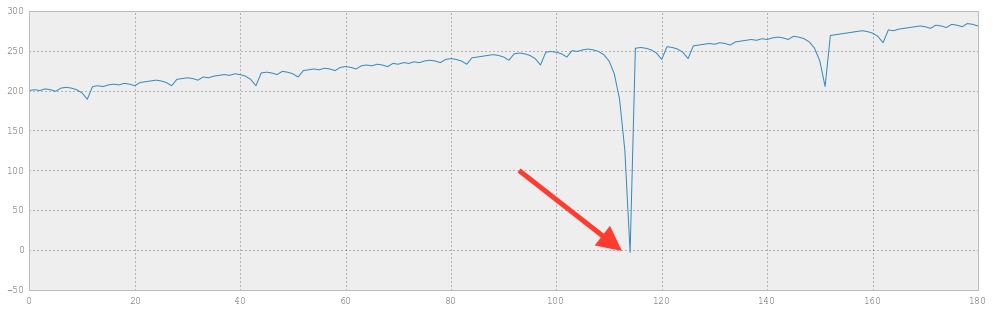
Tento graf ilustruje prečo je táto metóda problematická. Nestáva sa to vždy, ale občas sa stane, že nasleduje rovnaká farba veľa ťahov po sebe. V závislosti od počiatočného rozpočtu vždy existuje počet opakovaní ktorý je už likvidačný. Na úrovni 200€ je likvidačná 8x rovnaká farba zasebou.
| Ťah | Stávka | Kumulatívna strata | Stav účtu |
|---|---|---|---|
| 1 | 1 | 1 | 199 |
| 2 | 2 | 3 | 197 |
| 3 | 4 | 7 | 193 |
| 4 | 8 | 15 | 185 |
| 5 | 16 | 31 | 169 |
| 6 | 32 | 63 | 137 |
| 7 | 64 | 127 | 73 |
| 8 | 128 | 255 | -55 |
Pravdepodobnosť, že sa to stane je (19/37)^8 = 0,004835206373, čiže asi pol percenta. To môže vyzerať ako málo, ale treba si uvedomiť, že každý deň, podľa autora, hráme cca 180 hier!
Aby sme videli ako sa to prejaví v simulácii, pozrime sa na nasledujúci graf
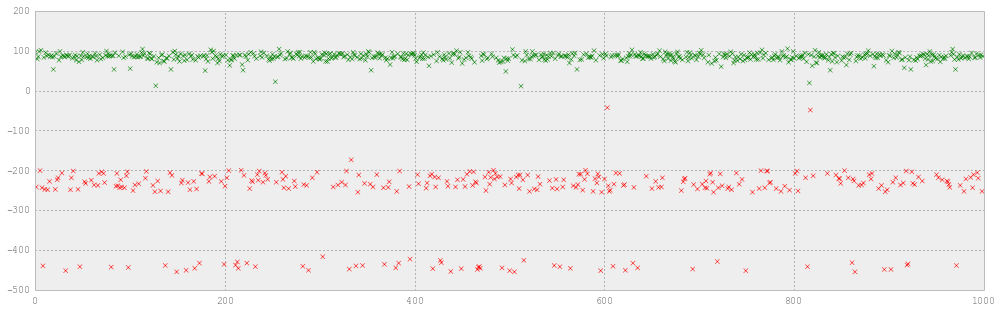
Tento graf ukazuje ako skončilo 1 000 hier, to sú cca 3 roky, 3 hodiny denne. Zelené krížiky sú hry ktoré skončili v pluse, červené, ktoré skončili v mínuse alebo na nule. Nula v tomto prípade znamená, že sme skončili s 200 eurami a za tie 3 hodiny sme nič nezarobili. Čiže oproti minimálnej mzde ste asi 9 eur v mínuse.
Ten istý program som pustil aj 10 000 krát, aby som získal presnejšie výsledky. Graf tu neukazujem, lebo je to len chaotickejšia verzia toho, ktorý tu už je. Zaujímavé sú však čísla. Minimálna výhra mi vyšla -455€, maximálna 111€ a pravdepodobnosť, že o všetko prídete cca na úrovni 34%. To znamená, že jedna tretina hier končí prinajlepšom na nule. Ale podstatný detail je, že nevyhráte 180€, ale len okolo 100€. Spolu to teda znamená, že v jednej tretine hier prerobíte 200€ a v dvoch tretinách zarobíte 100€, čo je dokopy cca 0€ keď sa to zráta a podčiarkne. To zhruba sedí s tým čo sa píše na Wikipedii v kolónke Expected value (on a $1 bet) (French), a síce, že očakávaná vyhra pri opakovanej stávke na jednu farbu je matematicky -$0.027.
V skratke, vyhráva kasíno. Ako vždy.
Pokračujte O čo vlastne ide a závery